John J Hopfield
Dense Associative Memory is Robust to Adversarial Inputs
Jan 04, 2017Abstract:Deep neural networks (DNN) trained in a supervised way suffer from two known problems. First, the minima of the objective function used in learning correspond to data points (also known as rubbish examples or fooling images) that lack semantic similarity with the training data. Second, a clean input can be changed by a small, and often imperceptible for human vision, perturbation, so that the resulting deformed input is misclassified by the network. These findings emphasize the differences between the ways DNN and humans classify patterns, and raise a question of designing learning algorithms that more accurately mimic human perception compared to the existing methods. Our paper examines these questions within the framework of Dense Associative Memory (DAM) models. These models are defined by the energy function, with higher order (higher than quadratic) interactions between the neurons. We show that in the limit when the power of the interaction vertex in the energy function is sufficiently large, these models have the following three properties. First, the minima of the objective function are free from rubbish images, so that each minimum is a semantically meaningful pattern. Second, artificial patterns poised precisely at the decision boundary look ambiguous to human subjects and share aspects of both classes that are separated by that decision boundary. Third, adversarial images constructed by models with small power of the interaction vertex, which are equivalent to DNN with rectified linear units (ReLU), fail to transfer to and fool the models with higher order interactions. This opens up a possibility to use higher order models for detecting and stopping malicious adversarial attacks. The presented results suggest that DAM with higher order energy functions are closer to human visual perception than DNN with ReLUs.
Dense Associative Memory for Pattern Recognition
Sep 27, 2016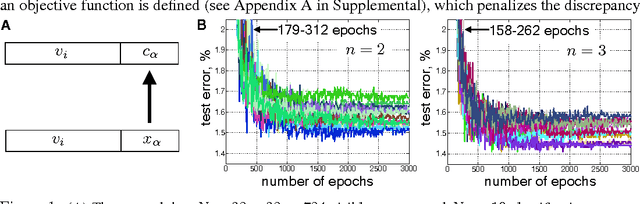
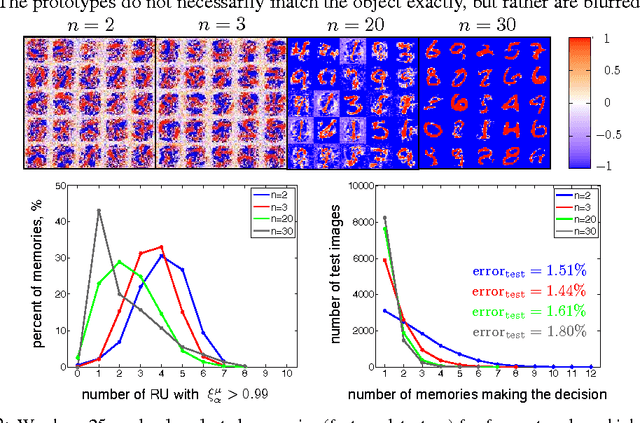
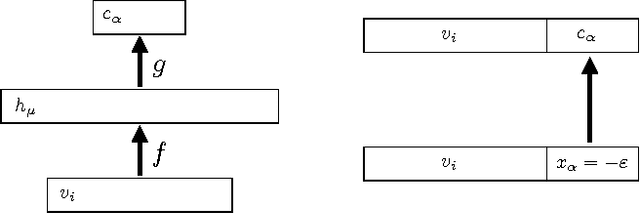
Abstract:A model of associative memory is studied, which stores and reliably retrieves many more patterns than the number of neurons in the network. We propose a simple duality between this dense associative memory and neural networks commonly used in deep learning. On the associative memory side of this duality, a family of models that smoothly interpolates between two limiting cases can be constructed. One limit is referred to as the feature-matching mode of pattern recognition, and the other one as the prototype regime. On the deep learning side of the duality, this family corresponds to feedforward neural networks with one hidden layer and various activation functions, which transmit the activities of the visible neurons to the hidden layer. This family of activation functions includes logistics, rectified linear units, and rectified polynomials of higher degrees. The proposed duality makes it possible to apply energy-based intuition from associative memory to analyze computational properties of neural networks with unusual activation functions - the higher rectified polynomials which until now have not been used in deep learning. The utility of the dense memories is illustrated for two test cases: the logical gate XOR and the recognition of handwritten digits from the MNIST data set.
* Accepted for publication at NIPS 2016
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge